Par Curve, Spot Curve, and Forward Curve

When you hear someone talk about “the yield curve”, they usually mean the par yield curve (and, more specifically, the par yield curve for risk-free bonds (e.g., the U.S. Treasury par curve)), but there are occasions when they might mean the spot yield curve or the forward yield curve.  We’ll go through a description of each curve, how they’re related (and how they differ), and, finally, what they look like.  In all cases, remember that we’re talking about yields on bonds, so the values quoted for yields will be bond equivalent yields (BEYs) (as opposed to, say, effective annual yields (EAYs)).

Par Curve

The par curve gives the yield to maturity (YTM) for (coupon-paying) bonds at each maturity: the single discount rate that you would use to discount all of the bond’s cash flows to get today’s market price.  (In other words, it’s the IRR vs. maturity curve for bonds.)  If you recall that when the YTM equals the bond’s coupon rate then the bond sells at par, then you’ll recognize the reason that this is called the par curve: it gives the coupon rate that a bond with a given maturity must pay to sell at par today.  Because there usually aren’t bonds on the market at every maturity (e.g., there’s not likely to be a bond with exactly 4.5 years to maturity, and another with exactly 13.5 years to maturity, and so on), the par curve is constructed by using whatever maturities are available in the market, and then using some mathematical technique to interpolate (or extrapolate) to get the remaining YTMs.  Therefore, different sources may have slightly different values for the yields.

One way that the par curve is used is in computing nominal spreads for bonds.  The nominal spread is simply the difference in the YTMs of two bonds with the same maturity, usually a risky bond (e.g., a corporate bond) and a risk-free bond (e.g., a Treasury).  The par curve is also the starting point for developing the spot curve and the forward curve.

Spot Curve

Whereas the par curve gives a yield that is used to discount multiple cash flows (i.e., all of the cash flows – coupons and principal – for a coupon-paying bond), the spot curve gives a yield that is used to discount a single cash flow at a given maturity (called a spot payment; hence: spot curve); it gives the YTM for zero-coupon (as opposed to coupon-paying) bonds.  Thus, to determine the price of a coupon-paying bond, instead of discounting all of the cash flows at the same rate – the bond’s YTM – you could discount the first coupon payment at the spot rate for its maturity, and the second coupon payment at the spot rate for its maturity, and so on.  The key that links the spot curve to the par curve is that you have to get the same price whether you use the par curve or the spot curve (otherwise, there would be an arbitrage opportunity).  The spot curve is derived from the par curve with this relationship in mind; the process to derive the spot curve is called bootstrapping (discussed below).

A common use for the spot curve is in computing the Z-spread for a bond.  A constant spread is added to each point on the spot curve, and these modified discount rates are used to determine the price of the bond: the amount of the spread is adjusted until the discounted price equals the market price.  The spot curve is also used to develop the forward curve.

Forward Curve

The forward curve is similar to the spot curve (from which it is derived) in that it discounts a single payment.  The difference is that it doesn’t discount that payment back to today; instead, it discounts it back one period (six months, generally).  Thus, the one-year forward rate is the rate used to discount a single payment one year from today back to six months from today; the eight-year forward rate is the rate used to discount a single payment eight years from today back to seven-and-one-half years from today.

The forward curve can be used to determine rates for FRAs, for example, where arbitrage ensures that the proper rates are used; the derivation of the forward curve from the spot curve observes the no-arbitrage condition.

Bootstrapping: Deriving the Spot Curve from the Par Curve

Suppose that the first few values on the par curve are:

Maturity (Years)	Par Yield
0.5	2.0000%
1.0	2.4000%
1.5	2.7600%
2.0	3.0840%
2.5	3.3756%
3.0	3.6380%

The six-month spot yield (\(s_1\), the spot rate for the first (six-month) period) is easy: it’s equal to the six-month par yield, 2.00% (because a six-month bond has only one payment).  To compute the one-year spot yield (\(s_2\)), we have to discount the payments on a one-year (par) bond with an annual coupon of 2.40%, then solve for the one-year discount rate (remember that these yields are BEY, that we’re discounting each individual payment by the spot rate for its maturity, and that a bond that pays a par coupon rate sells at par ($1,000)).  If the annual coupon rate is 2.40%, then the annual coupon payment is $24.00 (= 2.40% × $1,000), the semiannual coupon payments are $12.00 (= $24.00 ÷ 2) each, and we have:

\begin{align}$1,000\ &=\ \dfrac{$12.00}{1\ +\ \dfrac{2\%}{2}}\ +\ \dfrac{$1,012.00}{\left(1\ +\ \dfrac{s_2}{2}\right)^2}\\
\\
$1,000\ &=\ $11.88\ +\ \dfrac{$1,012.00}{\left(1\ +\ \dfrac{s_2}{2}\right)^2}\\
\\
$988.12\ &=\ \dfrac{$1,012.00}{\left(1\ +\ \dfrac{s_2}{2}\right)^2}\\
\\
\left(1\ +\ \dfrac{s_2}{2}\right)^2\ &=\ \dfrac{$1,012.00}{988.12}\ =\ 1.0242\\
\\
1\ +\ \dfrac{s_2}{2}\ &=\ \sqrt{1.0242}\ =\ 1.012012\\
\\
s_2\ &=\ 2.4024\%
\end{align}

To compute the 1½-year spot yield (\(s_3\)), we use the 1½-year par bond with a 2.76% (annual) coupon, or a semiannual coupon payment of $13.80 (= 2.76% × $1,000 ÷ 2):

\begin{align}$1,000\ &=\ \dfrac{$13.80}{1\ +\ \dfrac{2\%}{2}}\ +\ \dfrac{$13.80}{\left(1\ +\ \dfrac{2.4024\%}{2}\right)^2}\ +\ \dfrac{$1,013.80}{\left(1\ +\ \dfrac{s_3}{2}\right)^3}\\
\\
s_3\ &=\ 2.7669\%
\end{align}

The remainder of the spot yields are computed in the same (tedious) manner:

\begin{align}s_4\ &=\ 3.0974\%\\
\\
s_5\ &=\ 3.3975\%\\
\\
s_6\ &=\ 3.6701\%\\
\end{align}

Deriving the Forward Curve from the Spot Curve

Deriving forward yields from spot yields is quite similar to deriving spot yields from par yields, though a bit easier; it is covered in full in Calculating Forward Rates (from Spot Rates).

Some Insight into these Curves

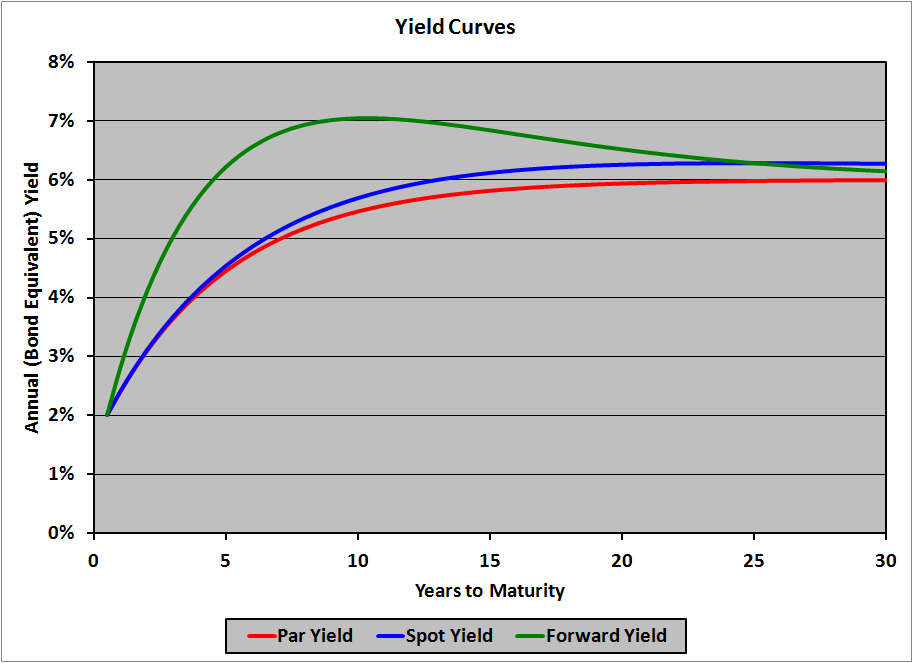
You can think of the par yield for a given maturity as a sort of average of the spot yields for all maturities up to and including the par yield’s maturity.  Thus, if the par curve is increasing, so par yield n is greater than par yield n – 1, then spot yield n must be above par yield n; the spot curve will lie above the par curve.  If the par curve is decreasing, the spot curve will lie below the par curve.  If the par curve increases, then decreases, the spot curve will cross it at its highest point.  (This is very similar to marginal and average cost from economics.)

Similarly, if the spot curve is increasing, the forward curve will lie above it, and if the spot curve is decreasing the forward curve will lie below it; the forward curve will cross from above to below at the highest point of the spot curve.

Here is a graph showing a (hypothetical) par curve, and the corresponding spot and forward curves:

The par curve is increasing everywhere (a normal yield curve), so the spot curve is above it everywhere.  The spot curve is increasing up to 25 years, then starts to decrease; thus, the forward curve is above it until 25 years, then crosses to below it.